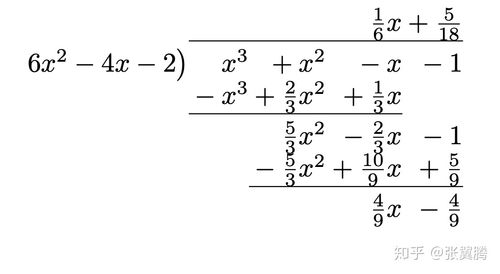最大公因式:探究数学中的重要概念
副标题:揭示数学公因式的本质与运用
在数学领域中,最大公因式是一个重要的概念,它可以帮助我们简化乘法运算,提高计算效率。今天,我们将深入探讨最大公因式的本质以及如何灵活运用它来解决实际问题。
最大公因式的定义与性质
最大公因式是指几个整数中,最大能够整除它们的数,也就是它们的最大公约数。最大公因式在数学中具有广泛的应用,它可以用于求解最大公约数、最小公倍数等问题。
最大公因式的性质与运用
最大公因式的性质非常多样化,下面列举几个常见的性质:
1. 最大公因式一定为整数
2. 最大公因式可以用来求解最大公约数和最小公倍数
3. 最大公因式可以用于简化乘法运算
如何使用最大公因式求解最大公约数和最小公倍数?
要使用最大公因式求解最大公约数和最小公倍数,我们需要先将两个或多个整数分解质因数。然后,我们可以通过求它们的最大公因数和最小公倍数来解决问题。
最大公因式的实际应用
最大公因式在实际生活中具有广泛的应用,下面列举几个实际应用:
1. 求解最大公约数:在购物时,我们可以使用最大公因式来计算购买商品的最大数量,从而享受更大的优惠。
2. 求解最小公倍数:在制定计划时,我们可以使用最小公倍数来计算完成任务所需的最短时间,从而提高工作效率。
结论
总之,最大公因式是数学中一个重要的概念,它在求解最大公约数和最小公倍数等问题中具有广泛的应用。通过深入理解最大公因式的性质和实际应用,我们可以更好地应用数学知识来解决实际问题。